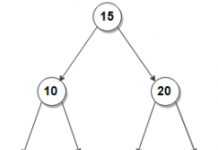
Binary search tree or BST is a node based tree in which each node has two children, we call it as left and right child. The top most node is called the root of the tree. The children of a node also have their own child nodes. It is a nested tree in which each branch has its two (binary) of its own child branches.
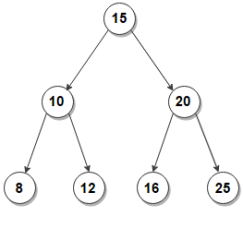
As you can observe in the above binary search tree that the left node/child has lesser value than the parent node and right node has greater value than the parent node. So this is a convention we follow while creating or using binary search tree so that searching, inserting and deleting in the binary search tree is easier to implement and also time complexity is less than traversing the complete array.
Also, No duplicates allowed in Binary Search Tree.
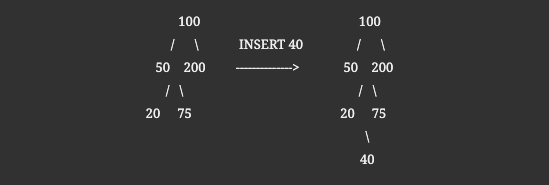
Insertion in Binary Search Tree
Insertion is always done at the ‘leaf’ node that is the bottom most suitable node. Once the leaf node is found then the value is entered as a child node to that leaf node.
Python Code For Insertion
- Check for root.
- If inserting element is less than root, recursively check for left node, else recursively check for right node
- Reached end? Insert to current node’s left node if less value than current node key, else insert to right.
class Node:
def __init__(self,key):
self.right = None
self.left = None
self.val = key
def insert(root,node):
if root is None:
root = node
else:
if node.val > root.val:
if root.right is None:
root.right = node
else:
insert(root.right, node)
else:
if root.left is None:
root.left = node
else:
insert(root.left, node)So basically, we have created a class Node and all nodes/branches of the binary search tree will behave like the objects of this class Node.
For inserting value in the binary search tree, we have created a member function which operates recursively and inserts the key at the desired position.
Searching a key in Binary Search Tree
For searching a key in Binary Search Tree, check for root value, if root value is equal to the key return root. If key is smaller than the root value check recursively for the left node, else for right node.
- Check the root
- If key is smaller than root value, check recursively for left node, else for right node
- Return true when element found, else return false.
Python code for searching
def search(root,key):
##when root is null or key is present
if root is None or root.val==key:
return root
else:
if key > root.val:
##when root value is smaller
return search(root.right, key)
##when root value is larger
return search(root.left,key)Deleting a key in Binary Search Tree
There are three cases possible for deleting a key in a binary search tree
1.Deleting a leaf, that is the bottommost element. Remove the element from the tree simply.

2. Deleting a node with a single child node. Delete the element and copy the contents of child node to that element position

3. Deleting a node with two child node/elements. Find the inorder successor and copy the contents of it to the node and delete the inorder successor. If the inorder successor of the node is empty, then we can use inorder predecessor too.
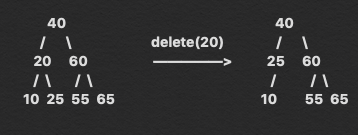
Inorder Successor
Inorder successor of a a node in a binary search tree is the smallest key greater than the input node.
Deletion of key python code
# Returns the node with min value in the tree
def minValue(node):
current = node
#looping down to leftmost leaf
while(current.left is not None):
current = current.left
return current
#Given a binary search tree,key . Deletes the key from the binary search tree.
def delete(root, key):
if root is None:
return root
#if key is larger, then it lies in right subtree
if key > root.val:
root.right = delete(root.right,key)
#if key is smaller, then it lies in left subtree
elif key < root.val:
root.left = delete(root.left,key)
#key is same as the root's value
else:
#node with one child node or none child node
if root.left is None:
temp = root.right
root = None
return temp
elif root.right is None:
temp = root.left
root = None
return temp
#Node with two child node
temp = minValue(root.right) #Get inorder successor's
root.val = temp.val
#Delete the inorder successor
root.right = delete(root.right,temp.val)


















![Pepcoding : A platform to learn coding [it’s FREE!!] pepcoding-logo](https://codingee.com/wp-content/uploads/2021/05/logo-218x150.png)