Write a C program to convert a matrix to a sparse matrix and perform addition on two sparse matrices.

If most of the value of a matrix is 0, then it is called a sparse matrix. There are lesser non-zero elements thus lesser memory is utilised and we can save computational time by logically designing a data structure that only traverses non-zero elements.

#include <stdio.h>
void addition(int ktemp[3][100], int ltemp[3][100], int k, int l);
int main()
{
    int a[20][20], ktemp[3][100], n, m, count = 0, i, j, k = 0, b[20][20], ltemp[3][100], l = 0, p, q;

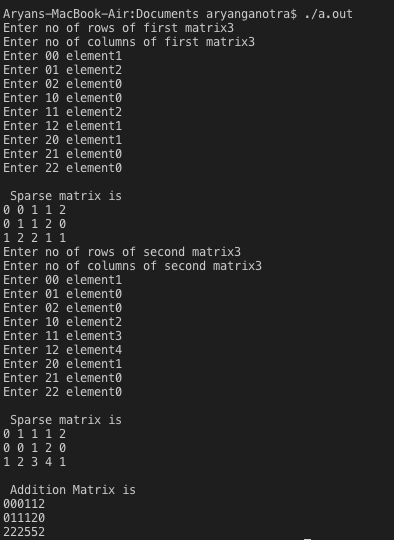
    printf("Enter no of rows of first matrix");
    scanf("%d", &n);
    printf("Enter no of columns of first matrix");
    scanf("%d", &m);
    for (i = 0; i < n; ++i)
    {
        for (j = 0; j < m; ++j)
        {
            printf("Enter %d%d element", i, j);
            scanf("%d", &a[i][j]);
            if (a[i][j] != 0)
            {
                ktemp[0][k] = i;
                ktemp[1][k] = j;
                ktemp[2][k] = a[i][j];
                k++;
            }
        }
    }
    printf("\n Sparse matrix is \n");
    for (i = 0; i < 3; i++)
    {
        for (j = 0; j < k; j++)
        {
            printf("%d ", ktemp[i][j]);
        }
        printf("\n");
    }

    printf("Enter no of rows of second matrix");
    scanf("%d", &p);
    printf("Enter no of columns of second matrix");
    scanf("%d", &q);
    if (p != m || q != n)
    {
        printf("\n Addtition can be performed on matrix of same order");
    }
    else
    {
        for (i = 0; i < n; ++i)
        {
            for (j = 0; j < m; ++j)
            {
                printf("Enter %d%d element", i, j);
                scanf("%d", &b[i][j]);
                if (b[i][j] != 0)
                {
                    ltemp[0][l] = i;
                    ltemp[1][l] = j;
                    ltemp[2][l] = b[i][j];
                    l++;
                }
            }
        }

        printf("\n Sparse matrix is \n");
        for (i = 0; i < 3; i++)
        {
            for (j = 0; j < l; j++)
            {
                printf("%d ", ltemp[i][j]);
            }
            printf("\n");
        }

        addition(ktemp, ltemp, k, l);
        return 0;
    }
}

void addition(int ktemp[3][100], int ltemp[3][100], int k, int l)
{
    int i = 0, j = 0, sparse[3][100], x = 0;

    while (i < k && j < l)
    {
        if ((ktemp[0][i] == ltemp[0][j]) && (ltemp[1][j] == ktemp[1][i]))
        {
            printf("Entered this");
            sparse[0][x] = ktemp[0][i];
            sparse[1][x] = ktemp[1][i];
            sparse[2][x] = ltemp[2][j] + ktemp[2][i];
            x++;
            i++;
            j++;
        }
        else
        {
            if (ktemp[0][i] < ltemp[0][j])
            {
                sparse[0][x] = ktemp[0][i];
                sparse[1][x] = ktemp[1][i];
                sparse[2][x] = ktemp[2][i];
                x++;
                i++;
            }

            else
            {
                if ((ktemp[0][i] == ltemp[0][j]) && (ktemp[1][i] < ltemp[1][j]))
                {
                    sparse[0][x] = ktemp[0][i];
                    sparse[1][x] = ktemp[1][i];
                    sparse[2][x] = ktemp[2][i];
                    x++;
                    i++;
                }
                else
                {
                    sparse[0][x] = ktemp[0][j];
                    sparse[1][x] = ktemp[1][j];
                    sparse[2][x] = ktemp[2][j];
                    x++;
                    j++;
                }
            }
        }
    }

    while (i < k)
    {
        sparse[0][x] = ktemp[0][i];
        sparse[1][x] = ktemp[1][i];
        sparse[2][x] = ktemp[2][i];
        x++;
        i++;
    }
    while (j < l)
    {
        sparse[0][x] = ktemp[0][j];
        sparse[1][x] = ktemp[1][j];
        sparse[2][x] = ktemp[2][j];
        x++;
        j++;
    }

    printf("\n Addition Matrix is \n");
    for (i = 0; i < 3; i++)
    {
        for (j = 0; j < x; j++)
        {
            printf("%d", sparse[i][j]);
        }
        printf("\n");
    }
}

Learning –  

Time complexity traversing simple matrix – O(n^2)

Time complexity traversing sparse matrix – O(n)