Introduction to heap
- Heap are complete binary tress. By complete, I mean each node except the leaf nodes has two children.
- Binary heaps are represented using array data structure.
- Unlike binary search tree, duplicates are allowed in heap.
- Max Heap – Value of each node must be greater than or equal to its children.
- Min Heap – Value of each node must be smaller than or equal to its children.
- Like a complete binary tree, height of the binary heap is also Log(n).
- If a node is at index i in the array then its left child is present at index 2*i and right child at index 2*i+1.
- Parent of the node at index i is present at [i/2].
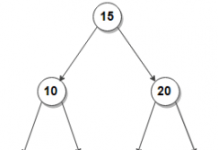
Example:-
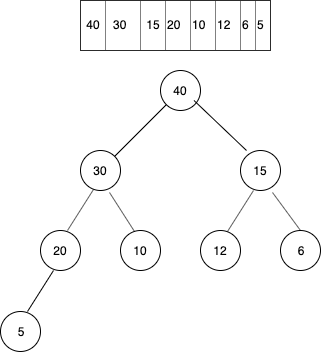
Inserting in a heap
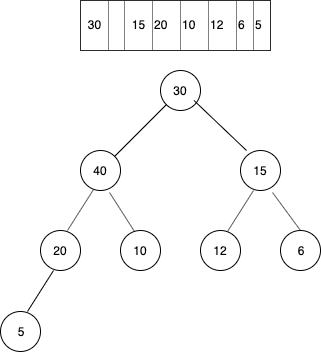
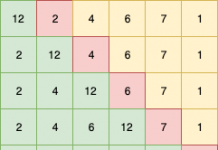
Consider the heap given below
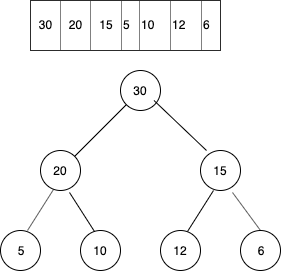
Inserting element 40
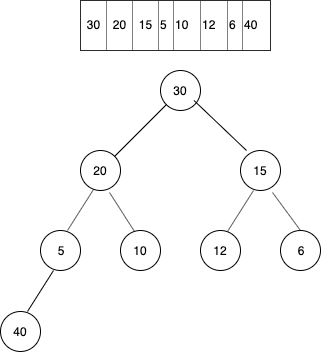
But this is not behaving like a heap as element 5 is smaller than its child 40. So we compare and swap 40 with its parent till it’s parent is greater.
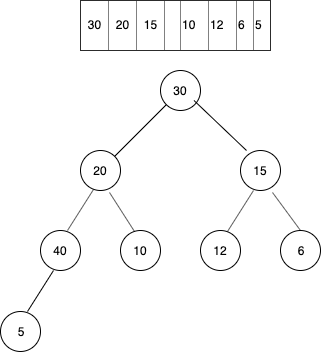
40 and 5 are swapped . Also in the heap array element 40 present at position 8 (index is taken from 1, and not 0), is swapped with element 5(it’s parent) present at index 8/2 = 4.
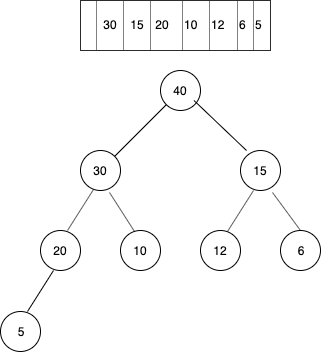
We will continue comparing element 40 with parent nodes, and keep swapping if parent is smaller than the child.
Final outcome
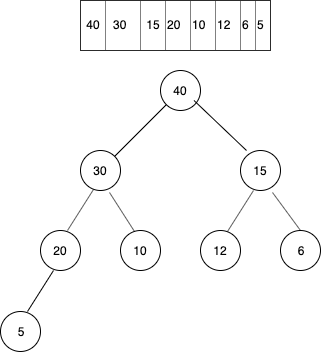
C Program to insert an element in a heap
void insert(int A[], int n)
{
int i = n, temp;
temp = A[i];
while(i>1 && temp>A[i/2])
{
A[i] = A[i/2];
i = i/2;
}
A[i] = temp;
}
Time complexity of inserting an element in a heap is O(logn).
Creating a heap
Creating a heap is similar to inserting an element in an existing heap.
Let us try to create a heap from an array.
I’ll show the code first and then explain.
int A[] = {0,1,3,2,4,5,6,10};
int n, i;
A[0] = 0;
for(i=2;i<=7;i++)
{
insert(A,i);
}So here we are creating a heap from array A. Element 0 is added for reference only as we are considering index from 1. We take a heap with only one element at first i.e element 1.
So now we have to just call the insert function on the above existing heap and this will create a heap for the remaining elements of array A.
Time complexity for inserting an element is O(logn), therefore for creating a heap, that is, inserting n elements is O(nlogn).
Deleting an element from Heap
A point to remember is that always the root node or first element of the heap array is deleted.
Procedure
- Remove the root node.
- Assign the last element to the root
- Now compare this new root element with its children. Swap this root element with its child if it is smaller the corresponding child.
- Continue till it is no further smaller than the child nodes.
Example
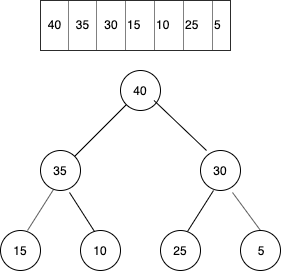
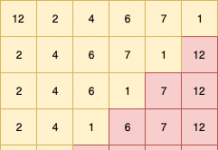
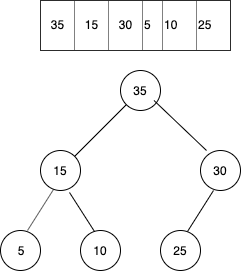
Consider the heap given below. As stated the root node element 40 must be deleted.
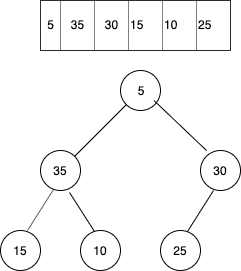
So our first step is to replace value at root with the value at the rightmost leaf node, that is, 5 here.
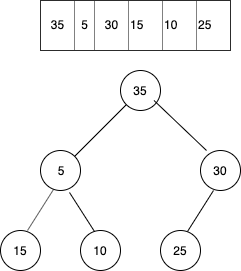
As child 35 was greater than parent 5 so swapped 35 and 5
Similarly swapped 5 and 15 too as child 15 was greater than 5.
Final outcome
C Program for deletion from a heap
int delete(int A[], int n)
{
int val, last, i, j, temp;
val = A[1];
last = A[n];
A[1] = last;
i = 1;
j = 2*i;
while(j<n-1)
{
if(A[j+1]>A[j])
{
j = j+1;
}
if(A[i]<A[j])
{
temp = A[i];
A[i] = A[j];
A[j] = temp;
i=j;
j=2*i;
}
else
{
break;
}
}
A[n] = val;
return val;
}Heap Sort
Heap sort is nothing but storing the deleted root element at the end of the vacant space in array.
Consider the above example.
We will delete all the root nodes one by one and assign the value of that root node at the end of the array like this.
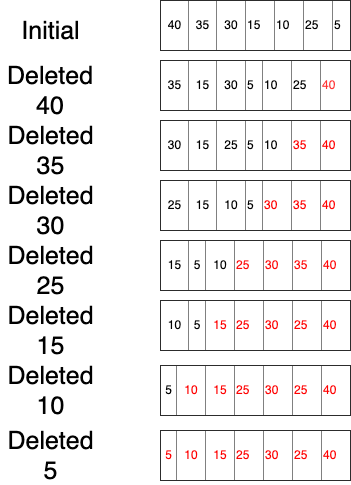
It can be interpreted that at the end , we obtain a sorted array. This is the way heap sort algorithm works.
Time complexity of heap sort is O(nlogn) as time complexity of deleting n elements is also O(nlogn).
Heapify
Heapify is a similar but better and faster approach for creating a heap
Difference
- Start traversing from rightmost element in the array .
- Time complexity is O(n) whereas for general approach is O(nlogn).
Binary heap as priority queue
Priority queue is a queue in which every element is marked with a priority or rank.
Element with higher priority is deleted first.
Problem – Deleting an element includes finding the element(O(n)) and then shifting elements(O(n)) . So a time complexity is O(n) which could be of significance with much larger data.
Solution – Using binary heap or representing data in the form of binary heap. As we know, in binary heap only the root node can be deleted and element of higher priority will always be at the root node, therefore time complexity of deleting root node from a binary heap is O(logn) which is significantly better than the general case.



















![Pepcoding : A platform to learn coding [it’s FREE!!] pepcoding-logo](https://codingee.com/wp-content/uploads/2021/05/logo-218x150.png)