Introduction
A flock of birds, of a school of fish moves in a very characteristic manner and the intricacies of their motion as a whole is not easy to define and each bird’s path would have to be scripted individually. The Boids’ algorithm was given by Craig Reynolds in 1987 as an alternative to the tedious task of defining the motion of all the objects of the system.
The aim of the project is to simulate and replicate the behavior of flocks of birds. The focus is on the behavior of each individual bird instead of interactions of an entire flock.
Literature Review
The Boids Algorithm
The Boids program consists of a group of objects(birds) each having their position, velocity and orientation.
With only three rules, we can specify the behavior of three birds.
- Seperation
- Alignment
- Cohesion
Seperation
Each boid tries to avoid running into other boids. If it gets too close to another boid it will steer away from it, hence to prevent overcrowding.
Alignment
Birds try to change their position so that it corresponds with the average alignment of other nearby birds. Each bird flies in some direction, when they see others, this rule gets each bird to try to align their direction based on their immediate neighbor.
Cohesion
Every bird attempts to move towards the average position of other nearby birds, that is, each bird tries to stay close to the other birds in the mass. When they register their neighbors, this rule tries to get each to come to the center of their neighbors defined space.
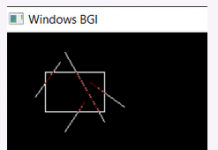
Quadtree
The decisions taken by a particular boid affects the it’s path. It is only intuitive to think that this decision would be based on the neighbouring boids rather than all of the boids in the system.
Thus, we need to calculate the neighbors of each boid. In a system with many objects, calculating the neighbours of each and every boid will be a costly operation and the time complexity will be O(n2), as we need to consider all the n*n objects in question.
This approach is quite inefficient, as we can see that for a mere 100 objects in the system, we will need 10,000 computations.
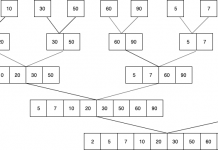
This can be optimised by a data structure called Quadtree, which is a data structure most often used to partition a two-dimensional space by recursively subdividing it into four quadrants or regions. The above problem can be solved in nlogn time which is very efficient as compared to n2 time. A quadtree is a tree data structure in which each internal node has exactly four children. It can be used to partition the space into buckets. Some of the properties of quadtrees are :
- They decompose space into adaptable cells
- Each cell (or bucket) has a maximum capacity. When maximum capacity is reached, the bucket splits
- The tree directory follows the spatial decomposition of the quadtree.
The 4 children of a quadtree divide the region covered by that node into four quadrants, commonly known as the north-west quadrant, the north-east quadrant, the south-east quadrant and the south-west quadrant.
The Quadtree data structure can be represented by the following class:
class QuadTree {
constructor(boundary, capacity) {
this.capacity = capacity;
this.objects = [];
this.subdivided = false;
this.boundary = boundary;
this.northEast = null;
this.northWest = null;
this.southEast = null;
this.southWest = null;
}
show()
query(range, found)
contains(point)
subdivide()
insert(point)
}
The data members can be explained as follows:-
- Capacity: The number of objects that a node can accommodate.
- Objects: The objects that are held by a particular node of the Quadtree.
- Subdivided: A boolean flag indicating whether the node has been subdivided into the four quadrants.
- northEast, northWest, southEast, southWest: references to the four subdivided quadtrees of a node.
The member functions can be explained as follows:
- show(): This is to draw the quadtree region on the canvas.
- query(): This function queries the quadtree data structure to get all the objects in the area bounded by range. The time complexity of this function is O(logn) and this is what makes the difference between the naive approach of looking at all particles of the system and using quadtree to optimize the computation.
- contains(): Checks if a point is contained in the region of that particular node. This function is of importance as we need to check if a point can be inserted into a node or not.
- subdivide(): This function is used to subdivide the quadtree into the four quadrants. It sets the boolean subdivided to true and the references northEast, northWest, southEast and southWest are initialized with quadtrees of their own.
- insert(): this function inserts a particular object into the quadtree. If the capacity of a node is not reached, then the object is inserted into that node, otherwise it is accommodated into one of the four quadrants. This function is recursive in nature.
In the above screenshot, we can see the quadtree Data structure and its recursive nature.
Code Analysis
The complete code can be viewed here on this github link, and the demo of the project can be seen here.
The important functions of the boid’s algorithm are explained below:
Alignment
align(nearby) {
let sf = createVector();
let total = 0;
for (let boid of nearby) {
if (boid === this) continue;
sf.add(boid.velocity);
total++;
}
if (total > 0) {
sf.div(total);
sf.setMag(this.maxSpeed)
sf.sub(this.velocity);
sf.limit(this.maxForce);
}
return sf;
}
The alignment function aligns the velocity of a boid to the average velocity of the neighbouring boids. The neighbouring boids are passed as an argument. The function returns the average velocity of all the neighbours.
Cohesion
cohesion(nearby) {
let sf = createVector();
let total = 0;
for (let boid of nearby) {
if (boid === this) continue;
sf.add(boid.position);
total++;
}
if (total > 0) {
sf.div(total);
sf.sub(this.position);
sf.setMag(this.maxSpeed)
sf.sub(this.velocity)
sf.limit(this.maxForce);
}
return sf;
}
This function is to make the boids attracted to the center of mass of the local flock, so that the flock moves together as one. The neighbouring boids are passed as an argument. The function returns the center of mass of the local flock.
Separation
separation(boids) {
let sf = createVector();
let total = 0;
let perceptionRadius = 24;
for (let boid of boids) {
if (boid === this) continue
let d = distance(boid, this);
if (boid != this && d <= perceptionRadius) {
let diff = p5.Vector.sub(this.position, boid.position);
diff.div(d);
sf.add(diff);
total++;
}
}
if (total > 0) {
sf.div(total);
sf.setMag(this.maxSpeed)
sf.sub(this.velocity)
sf.limit(0.3);
}
return sf;
}
Links
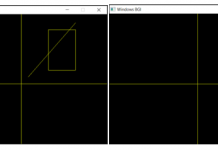
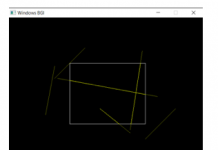
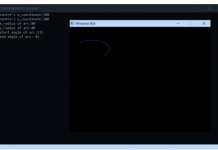
Screenshots
Conclusion
Watching as a massive collection of birds float across the sky like an unpredictable wave, it’s difficult to comprehend how birds can fly in formation without the aid of the high- tech location equipment.
Such patterns may look like the result of extrasensory communication, but they’re in fact the product of emergent animal group behaviour known as flocking. Every change of direction comes not as a result of an individual member of the flock, but rather of the snap decisions made by those individuals in response to the movements of their neighbours.
We have simulated the behaviour of flocks of birds to observe the pattern. With only a few simple rules, our program manages to generate a result that is complex and realistic enough.
References



















![Pepcoding : A platform to learn coding [it’s FREE!!] pepcoding-logo](https://codingee.com/wp-content/uploads/2021/05/logo-218x150.png)