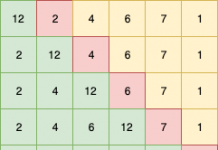
Example – A = [3,-1,-1,-1,7,-5,1,2]
Sub-arrays with sum 0= (3,-1,-1,-1), (-1,-1,7,-5) (Contiguous only)
Approach –
Naive approach O(n^2) – traverse through all subarrays and check the sum.
Optimal approach (O(n))
Create a dictionary/hash map/multi map with key as sum and ending index of all sub arrays with given sum as value.
Traverse through the array and add each element to a sum(initialise=0) variable and check that if the sum is present in the mapping, if present then the sub array from the indexes present in the mapping for that sum to the current index has sum = 0.
In simpler words, we traverse the given array, and maintain sum of elements seen so far. If sum is seen before, there exists at-least one sub-array with 0 sum which ends at current index and we print all such sub-arrays.



















![Pepcoding : A platform to learn coding [it’s FREE!!] pepcoding-logo](https://codingee.com/wp-content/uploads/2021/05/logo-218x150.png)